Programming Assignment 2
A2: Constant Propagation and Worklist Solver
1 Assignment Objectives
- Implement a constant propagation for Java.
- Implement a generic worklist solver, which will be used to solve the data-flow problem you defined, i.e., constant propagation.
In this programming assignment, you will implement the key parts of a constant propagation and a worklist solver on top of Tai-e. We introduce a lot of information in this document which is necessary for implementing a working constant propagation and worklist solver. Please read the document thoroughly.
Now, we suggest that you first setup the Tai-e project for Assignment 2 (in A2/tai-e/ of the assignment repo) by following Setup Tai-e Assignments.
2 Implementing Constant Propagation
2.1 Scope
In this assignment, you need to implement the constant propagation for values of int type. Note that in Java, actually the values of types boolean, byte, char, and short are also represented and computed as int values during run time, thus your analysis would also be able to handle the values of these types. Other primitive types (long, float, and double) and reference types (class types, array types, etc.) are out of scope, and you should ignore the values of these types.
For statements, as shown in page 247 of slides for Lecture 6, you only need to focus on assign statements whose left-hand side expressions are variables, and right-hand side expressions are:
- Constants, e.g.,
x = 1 - Variables, e.g.,
x = y - Binary expressions, e.g.,
x = a + b, andx = a >> b
Table 1 lists all binary operations (except logical) that you could perform on int values in Java, and you need to handle all these operators in your assignment.
| Kinds | Operators |
|---|---|
| Arithmetic | + - * / % |
| Condition | == != < > <= >= |
| Shift | << >> >>> |
| Bitwise | | & ^ |
We do not list logical operators, i.e., logical AND (&&) and OR (||) in above table, because in Java, these two operators do not have corresponding instructions in bytecode, and instead, they are implemented as branch statements. For example, such statement
a = b || c;
will be transformed to following semantically equivalent statements:
if (b) {
t = true; // t is temp variable
} else if (c) {
t = true;
} else {
t = false;
}
a = t;
As our constant propagation can handle assignments for constants (e.g., t = true) and variables (e.g., a = t), and branch statements (e.g., if (b) {...}), it can handle && and || automatically.
For the assign statements (again, whose left-hand side expressions are variables) with other right-hand side expressions, e.g., method calls (x = m(...)) or field loads (x = o.f), you should give them conservative (maybe imprecise) approximations, e.g., x = NAC. You will handle method calls and field loads more precisely in later assignments.
For the other statements that are not mentioned above (e.g., field store o.f = x which will be handled after we learn alias analysis), the transfer function is identity function.
2.2 Tai-e Classes You Need to Know
In this section, we first introduce the IR-related classes (pascal.taie.ir.*) and then the analysis-related classes (pascal.taie.analysis.*) you need to know for implementing constant propagation.
pascal.taie.ir.IRThis class is the central data structure of intermediate representation in Tai-e, and each IR instance contains the information for the body of a particular method, such as variables, parameters, statements, etc. You can obtain this information through its APIs, which are all commented in the source code.
pascal.taie.ir.exp.ExpYou have seen this interface in Assignment 1. In this assignment, you will need to handle more of its subclasses, as shown in this partial class hierarchy:
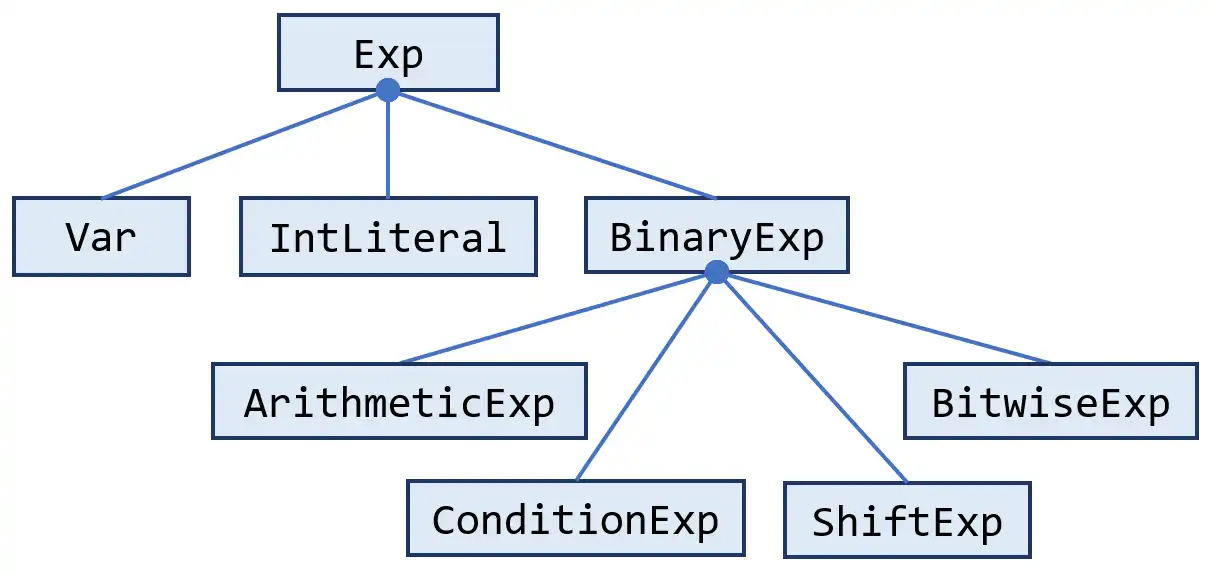
Now we introduce the classes in this figure.
pascal.taie.ir.exp.VarThis class represents the variables in Tai-e’s IR.
pascal.taie.ir.exp.IntLiteralFollowing Java Language Specification, we call constant values literals in Tai-e. Each instance of this class represents an integer literal in the program, and you can obtain the int value by calling its
getValue()method.pascal.taie.ir.exp.BinaryExpThis class represents binary expressions in the program. It has several subclasses, corresponding to different kinds of binary expressions as shown in Table 1, and each subclass contains an inner enum type which represents the operators supported by the expression class. For example,
ArithmeticExp.Oprepresents the operators ofArithmeticExp(arithmetic expressions), i.e.,+ - * /and%.Note that in Tai-e, both operands of
BinaryExpare of typeVar, e.g., statementx = y + 6;will be transformed to
%intconst0 = 6; // %intconst* are temp variables introduced x = y + %intconst0; // by Tai-e to hold constant int valuesin Tai-e’s IR. Such design simplifies the implementation of analyses, as you only need to consider one case (i.e., Var) for every operand of any
BinaryExp.pascal.taie.ir.stmt.DefinitionStmtIn this assignment, we use two terms assign statement and definition statement interchangeably.
This class is a subclass of
Stmt, and it represents all definition statements in the program, e.g.,x = yorx = m(...)wherexis defined. This class is very simple, and you could read its source code and comments to decide how to use it.pascal.taie.analysis.dataflow.analysis.DataflowAnalysisThis is the interface of concrete data-flow analyses and will be used by the analysis solver as you have seen in Assignment 1. In this assignment, you also only need to focus on the first 5 APIs, which will be invoked by the worklist solver you write.
pascal.taie.analysis.dataflow.analysis.constprop.ValueThis class represents the lattice values in constant propagation, i.e., (the lattice described in page 238 of slides for Lecture 6). Its code and comments are self-explaining. You should use these static methods to obtain instances of this class:
Value getNAC(): ReturnsNACValue getUndef(): ReturnsUNDEFValue makeConstant(int): Returns a constant for the given integer
pascal.taie.analysis.dataflow.analysis.constprop.CPFactThis class represents the data facts in constant propagation, i.e., the mapping from variables (
Var) to their lattice values (Value). This class provides various map-related operations, such as query/update key-value mappings, etc., and most of them are inherited frompascal.taie.analysis.dataflow.fact.MapFact. The APIs of both classes are commented in the source code, and you should read the source code and decide which APIs to use in this assignment.pascal.taie.analysis.dataflow.analysis.constprop.ConstantPropagationThis class implements
DataflowAnalysisand defines constant propagation. It is incomplete, and you need to finish it as explained in Section 2.3.
2.3 Your Task [Important!]
Your first task is to implement the following APIs of ConstantPropagation:
CPFact newBoundaryFact(CFG)CPFact newInitialFact()void meetInto(CPFact,CPFact)boolean transferNode(Stmt,CPFact,CPFact)
You have seen the above four APIs from Assignment 1, which are inherited from DataflowAnalysis. Note that when implementing newBoundaryFact(), for each method being analyzed, you should handle the parameters of the method properly, i.e., initialize their values to NAC (Question for you: Why do we do this?).
Hint:
As mentioned in Section 2.1, we focus on constant propagation for values of int type in this assignment. To achieve this, we provide an auxiliary method canHoldInt(Var) in ConstantPropagation to judge if a variable can hold values of int type, and you should use it to check if a parameter, and also other variables, are in the scope of this assignment. You should ignore the variables that are out of scope (e.g., float variables).
In addition, you need to implement these two auxiliary methods:
Value meetValue(Value,Value)This corresponds to the meet operator ⊓ defined in page 238 of slides for Lecture 6. You should invoke this method from
meetInto().Value evaluate(Exp,CPFact)This method evaluates the lattice value (
Value) for a right-hand side expression (Exp). You will need to handle three cases in this method as described in page 247 of slides for Lecture 6, and for other cases, it should returnNAC(also described in Section 2.1). You should invoke this method fromtransferNode().
Hints:
- As in Assignment 1, the design of
meetInto()might be a bit different from your expectation. To understand this design, please review relevant part in the document for Assignment 1. - The evaluation results of condition expressions (e.g.,
a == b) should be represented by1(fortrue) or0(forfalse). - For cases of division-by-zero (both
/and%), you should treat its result asUNDEF, e.g., forx = a / 0,xisUNDEF.
3 Implementing Worklist Solver
3.1 Tai-e You Need to Know
Similar to iterative solver, to implement worklist solver on Tai-e, you need to know DataflowResult, CFG, and Solver, which have been introduced in Assignment 1. Besides, you need to know:
pascal.taie.analysis.dataflow.solver.WorkListSolverThis class extends
Solverand implements worklist algorithm. It is incomplete, and to be finished.
3.2 Your Task [Important!]
Your second task is to finish two APIs of the solver classes mentioned above:
Solver.initializeForward(CFG,DataflowResult)WorkListSolver.doSolveForward(CFG,DataflowResult)- The worklist algorithm in the slides compares
old_OUTandOUT[B]to decide if the successors of a node need to be added to the worklist, which is not very efficient.DataflowAnalysis.transferNode()returns whether the transfer changes the OUT fact of the node on each call, and you could leverage this feature to avoid comparingold_OUTandOUT[B]. - Similar to iterative solver in Assignment 1, do not forget to initialize IN fact of each
StmtinSolver.initializeForward()(the same initial fact as in OUT).
You only need to focus on forward-related methods as constant propagation is a forward analysis. In initializeForward(), you should implement the first three lines in the algorithm in page 258 of slides for Lecture 6. You should implement the main part of worklist algorithm in doSolveForward().
Hints:
We have provided code skeletons for the above APIs, and your task is to fill in the part with comment "TODO – finish me".
4 Run and Test Your Implementation
You can run the analysis as described in Set Up Tai-e Assignments. In this assignment, Tai-e performs constant propagation for each method of input class, and outputs the analysis results, i.e., the data-flow information (lattice values of variables) in OUT fact of each Stmt:
The OUT facts are null as you have not finished the analysis yet. After you implement the analysis, the output should be:
In addition, Tai-e outputs the control-flow graphs of the methods it analyzes to folder output/. The CFGs are stored as .dot files, and can be visualized by Graphviz.
We provide class pascal.taie.analysis.dataflow.analysis.constprop.CPTest as the test driver for this assignment, and you could use it to test your implementation as described in Set Up Tai-e Assignments.
5 General Requirements
In this assignment, your only goal is correctness. Efficiency is not your concern.
DO NOT distribute the assignment package to any others.
Last but not least, DO NOT plagiarize. The work must be all your own!
6 Submission of Assignment
Your submission should be a zip file, which contains your implementation of
ConstantPropagation.javaSolver.javaWorkListSolver.java
7 Grading
You can refer to Grade Your Programming Assignments to use our online judge to grade your completed assignments.
The points will be allocated for correctness. We will use your submission to analyze the given test files from the src/test/resources/ directory, as well as other tests of our own, and compare your output to that of our solution.
Good luck!