Programming Assignment 5

A5: Context-Insensitive Pointer Analysis

Course “Static Program Analysis” @Nanjing University

Assignments Designed by Tian Tan and Yue Li

1 Assignment Objectives

Implement a context-insensitive pointer analysis for Java.
Implement on-the-fly call graph construction as part of pointer analysis.

In this programming assignment, you will implement a context-insensitive pointer analysis for Java on top of Tai-e. This pointer analysis builds a call graph on the fly. If your implementation is correct, you can observe that pointer analysis can build more precise call graphs than class hierarchy analysis (CHA) as described later.

In this assignment, we will teach you how to handle the Java features that are not covered in the lectures, i.e., static field, array, and static method, so that you will implement a pointer analysis that can handle all kinds of pointers in Java.

Now, we suggest that you first setup the Tai-e project for Assignment 5 (in A5/tai-e/ of the assignment repo) by following Setup Tai-e Assignments.

2 Implementing Pointer Analysis

2.1 Scope

You will implement the context-insensitive pointer analysis algorithm introduced in Lectures 9 and 10, in which the algorithm handles two kinds of pointers, i.e., local variables and instance fields, as well as instance method calls. To achieve a more practical pointer analysis, you will handle the other two kinds of pointers, i.e., static fields and array indexes, as well as static method calls in this assignment. We will introduce the analysis rules to handle these features in Section 2.2. These rules are very similar to (or even simpler than) the rules you have learnt in lectures, and you need to figure out how to implement them based on the pointer analysis algorithm.

2.2 New Rules

In this section, we introduce new pointer analysis rules to handle static fields, array indexes, and static method calls.

Static Fields. The handling of static fields is simple, i.e., we just need to pass values between the static field and the variable. We use $T . f$ to denote the pointer for static field T.f, and then define the rules to handle static field stores and loads as follows:

Kind	Statement	Rule	PFG Edge
Static Store	`T.f = y`	$o_{i} \in p t (y)$ $o_{i} \in p t (T . f)$	$T . f \leftarrow y$
Static Load	`y = T.f`	$o_{i} \in p t (T . f)$ $o_{i} \in p t (y)$	$y \leftarrow T . f$

Array Indexes. As explained in page 86 of the slides for Lecture 8, regular pointer analysis does not distinguish between loads and stores to different array indexes (locations). Suppose that $o_{i}$ represents an array object, then we use $o_{i} [*]$ to denote the pointer which points to all elements that are stored in any indexes of the array. Based on such treatment, we define the rules to handle array stores and loads:

Kind	Statement	Rule	PFG Edge
Array Store	`x[i] = y`	$o_{u} \in p t (x), o_{v} \in p t (y)$ $o_{v} \in p t (o_{u} [*])$	$o_{u} [*] \leftarrow y$
Array Load	`y = x[i]`	$o_{u} \in p t (x), o_{v} \in p t (o_{u} [*])$ $o_{v} \in p t (y)$	$y \leftarrow o_{u} [*]$

Static Methods. The handing of static methods is the same as that of instance methods, except that 1) we do not need to dispatch on the receiver object to resolve the callee, and 2) we do not need to pass the receiver object. Since static method calls do not require receiver object, its treatment is simpler than that of instance method calls as shown below:

Kind	Statement	Rule	PFG Edge
Static Call	`r = T.m(a1,...,an)`	$o_{u} \in p t (a_{j}), 1 \leq j \leq n$ $o_{v} \in p t (m_{r e t})$ $o_{u} \in p t (m_{p j}), 1 \leq j \leq n$ $o_{v} \in p t (r)$	$a_{1} \to m_{p 1}$ ... $a_{n} \to m_{p n}$ $r \leftarrow m_{r e t}$

2.3 Tai-e Classes You Need to Know

In this section, we first introduce the IR-related classes (pascal.taie.ir.*) and then the pointer-analysis-related classes (pascal.taie.analysis.pta.*) that you need to know to finish this assignment.

pascal.taie.ir.stmt.DefinitionStmt
You have seen this class in previous assignments. It represents all definition statements in the program, e.g., x = y and x = m(…). All pointer-affecting statements that you need to handle in this assignment are subclasses of this class, as shown in the figure below (you will handle the classes in red boxes).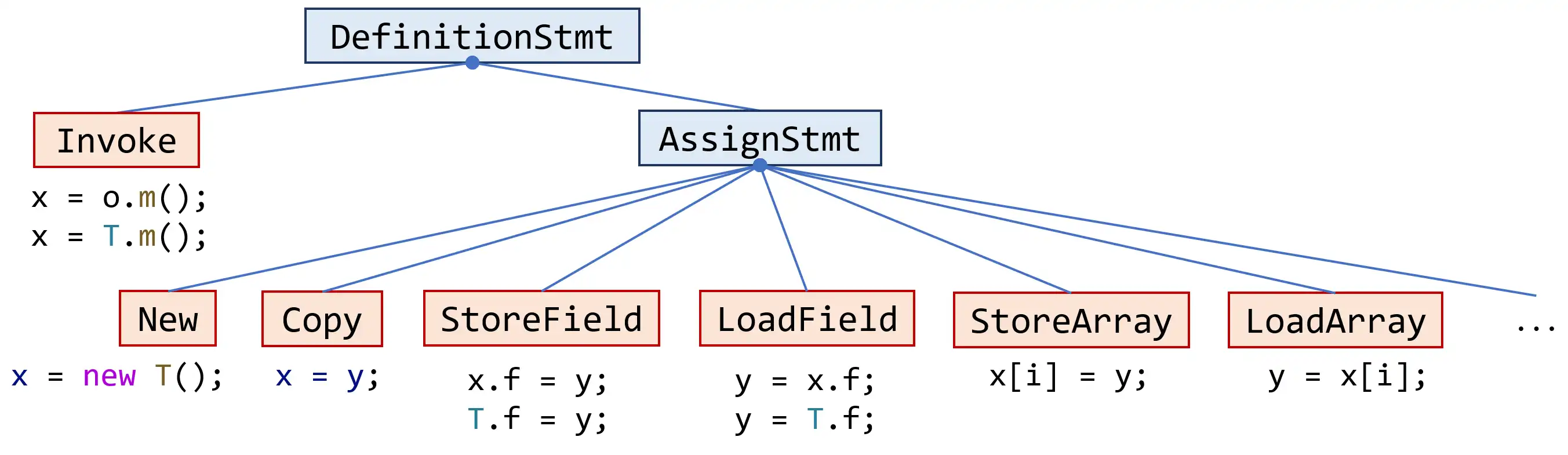
These classes are simple, and you could get familiar with them by reading the source code and comments. Note that Invoke represents both instance method calls and static method calls as you have seen in Assignment 4, and you can use its isStatic() method to check if the Invoke statement is a static or instance call. Similarly, LoadField and StoreField represent loads and stores of both instance and static fields. These two classes also provide isStatic() method to check if a LoadField/StoreField statement loads/stores a static or instance field.
pascal.taie.ir.exp.Var
You have seen this class before, which represents the variables in Tai-e’s IR. If a variable is the base variable of any instance field loads/stores, array loads/stores, or instance calls, then this class provides convenient APIs to find the relevant statements. For example, suppose we are analyzing the following code snippet:
```
x = y;
x.h = a;
x.g = z;
a = x.f;
b = y.f;
c = x.m();
d[i] = c;
e = d[i];
```
If var represents variable x, then var.getStoreFields() returns the field store statements at lines 2 and 3, var.getLoadFields() returns the field load statement at line 4, and var.getInvokes() returns the instance call at line 6; if var represents variable d, then var.getStoreArrays() returns the array store statement at line 7, and var.getLoadArrays() returns the array load statement at line 8.
These APIs ease the implementation of pointer analysis, and we strongly recommend you to use them in this assignment. You could read the source code and comments in class Var for more information.
pascal.taie.language.classes.JField
This class represents fields in the program.

Below we introduce pointer-analysis-related classes. These classes are generally simple, and you should read their source code and comments to decide how to use them.

pascal.taie.analysis.pta.core.heap.Obj
This class represents abstract objects in pointer analysis, i.e., the objects in points-to sets.
pascal.taie.analysis.pta.core.heap.HeapModel
This class represents heap models (i.e., heap abstraction) for heap objects. You can use its getObj(New) method to obtain the abstract object (i.e., Obj) for given New statement (i.e., allocation site). We adopt allocation-site abstraction as introduced in page 44 of the slides for Lecture 8, thus this method returns a unique abstract object for each New statement.
pascal.taie.analysis.pta.ci.PointsToSet
This class represents points-to sets, i.e., sets of Obj in pointer analysis. It is iterable, i.e., you could iterate the objects in a points-to set via a for loop:
```
PointsToSet pts = ...;
for (Obj obj : pts) ...
```
pascal.taie.analysis.pta.ci.Pointer
This class represents the pointers in the analysis, i.e., the nodes in the PFG (pointer flow graph). Each Pointer is associated with a PointsToSet, which can be obtained by calling getPointsToSet(). This class has four subclasses: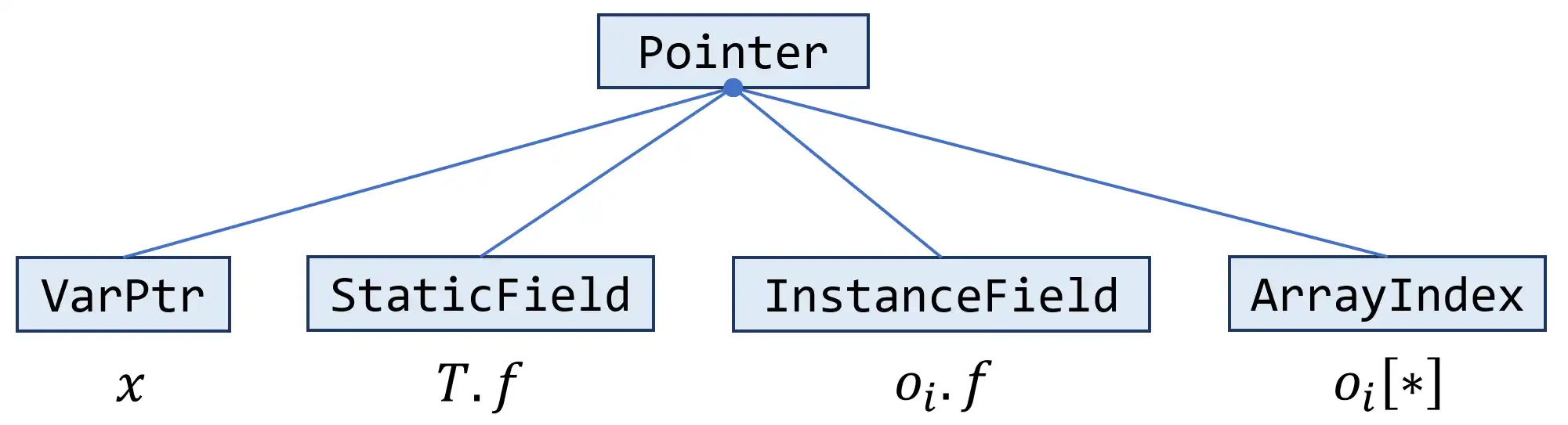
which corresponds to the four kinds of pointers in Java as introduced in page 82 of slides for Lecture 8.
pascal.taie.analysis.pta.ci.PointerFlowGraph
This class represents a pointer flow graph of the program. It also maintains the mappings from variables / static fields / instance fields / array indexes to corresponding pointers (i.e., PFG nodes), and thus you can obtain various Pointers from APIs of this class.
pascal.taie.analysis.pta.ci.WorkList
This class represents the worklist in pointer analysis algorithm. It has an inner record classopen in new window Entry which represents the entries in the worklist.
pascal.taie.analysis.pta.ci.Solver
This class implements a context-insensitive pointer analysis solver. It is incomplete, and you need to finish it as explained in Section 2.4.

In addition to the above classes, you also need to know classes JMethod, IR, InvokeExp, DefaultCallGraph, and Edge. Since these classes have been introduced in the previous assignment, we do not detail them here.

2.4 Your Task [Important!]

Your task is to finish class Solver. We have initialized work list, pointer flow graph, and call graph in Solver.initialize(), and stored them in Solver’s fields worklist, pointerFlowGraph, and callGraph, so that you can manipulate them. When you build call graph, you can use the APIs of DefaultCallGraph introduced in the previous assignment to modify the call graph. You need to finish the main part of the pointer analysis algorithm. Specifically, you will finish the following five APIs:

void addReachable(JMethod)
This method implements the AddReachable function given in page 119 of the slides for Lecture 10.
Hints:
1. Do not forget to handle static field loads/stores and static method calls in this method.
2. You can obtain the field to be loaded/stored by a LoadField/StoreField statement in this way:
```
LoadField stmt = ...;
JField field = stmt.getFieldRef().resolve();
```
3. To build call graph on the fly, you need to resolve the callees of the method calls. For your convenience, we provide method Solver.resolveCallee(Obj,Invoke) to resolve callees of static, virtual, interface, and special invocations in Java.
4. In addReachable(), you need to handle different kinds of statements using different logics. A reasonable way to implement such needs is visitor patternopen in new window. Tai-e’s IR provides natural support for visitor pattern. Specifically, Tai-e provides class pascal.taie.ir.stmt.StmtVisitor, the common interface for all Stmt visitors, which declares the visit operations for all kinds of statements. Besides, all non-abstract subclasses of Stmt implement an accept(StmtVisitor) method so that they can accept the visit from concrete visitors.
  In Solver, we have provided code skeleton for Stmt visitor (i.e., inner class StmtProcessor), created its instance in initialize(), and stored the instance in field stmtProcessor. If you choose to implement the logics of addReachable() via visitor pattern, then you should implement the relevant visit(…) methods in class StmtProcessor, and use it to process the statements in the reachable method. The return values of visit(…) methods are ignored in this assignment, thus you just need to return null when you implement visit(…) methods.
  If you are not familiar with visitor pattern, it is totally fine to implement addReachable() in your way.
void addPFGEdge(Pointer,Pointer)
This method implements the AddEdge function given in page 43 of the slides for Lecture 9.
void analyze()
This method implements the main part, i.e., the while loop, of the Solve function given in page 125 of the slides for Lecture 10.
Hint: Do not forget to handle array loads/stores in this method.
PointsToSet propagate(Pointer,PointsToSet)
This method merges two steps of the algorithm. It first computes the difference set ( $Δ = p t s - p t (n)$ ), then propagates $p t s$ into $p t (p)$ as described by the Propagate function in page 43 of the slides for Lecture 9. It returns $Δ$ as the result of the call.
void processCall(Var,Obj)
This method implements the ProcessCall function given in page 124 of the slides for Lecture 10.
Hints:
1. You will handle all kinds of instance method calls, i.e., virtual, interface and special calls in this method. The logic of handling interface and special calls are exactly the same as that of virtual calls (which you have learnt in the lectures). You can also use resolveCallee() mentioned above (instead of Dispatch in the algorithm) to resolve the callees of all kinds of instance method calls, i.e., virtual, interface and special calls.
2. For soundness, you should pass the objects pointed to by all returned variables (i.e., the variables appear in return statements) of a method to the LHS variables of its call sites. You can obtain the returned variables of a method through the relevant IR object.

We have provided code skeletons for the above APIs, and your task is to fill in the part with comment "TODO – finish me".

3 Run and Test Your Implementation

You can run the analysis as described in Set Up Tai-e Assignments. In this assignment, Tai-e performs context-insensitive pointer analysis for the program, and outputs the points-to sets of all kinds of pointers and the resulting call graph:

--------------Pointer analysis statistics:--------------

#var pointers: 0

#var points-to: 0

#static field points-to: 0

#instance field points-to: 0

#array indexes points-to: 0

#reachable methods: 0

#call graph edges: 0

----------------------------------------

Points-to sets of all variables

Points-to sets of all static fields

Points-to sets of all instance fields

Points-to sets of all array indexes

#reachable methods: 0

----------Reachable methods:----------

#call graph edges: 0

----------Call graph edges:----------

----------------------------------------

The points-to sets and call graph are empty as you have not finished the analysis yet. After you implement the analysis, the output should look like:

--------------Pointer analysis statistics:--------------

#var pointers: 13

#var points-to: 17

#static field points-to: 0

#instance field points-to: 0

#array indexes points-to: 0

#reachable methods: 5

#call graph edges: 6

----------------------------------------

Points-to sets of all variables

<A: void <init>()>/%this -> [NewObj{<B: A foo(A)>[0@L18] new A}, NewObj{<Example: void main(java.lang.String[])>[0@L4] new A}, NewObj{<Example: void main(java.lang.String[])>[3@L5] new B}]

<B: A foo(A)>/%this -> [NewObj{<Example: void main(java.lang.String[])>[3@L5] new B}]

<B: A foo(A)>/r -> [NewObj{<B: A foo(A)>[0@L18] new A}]

<B: A foo(A)>/temp$0 -> [NewObj{<B: A foo(A)>[0@L18] new A}]

<B: A foo(A)>/y -> [NewObj{<Example: void main(java.lang.String[])>[0@L4] new A}]

<B: void <init>()>/%this -> [NewObj{<Example: void main(java.lang.String[])>[3@L5] new B}]

<Example: void main(java.lang.String[])>/a -> [NewObj{<Example: void main(java.lang.String[])>[0@L4] new A}]

<Example: void main(java.lang.String[])>/b -> [NewObj{<Example: void main(java.lang.String[])>[3@L5] new B}]

<Example: void main(java.lang.String[])>/c -> [NewObj{<B: A foo(A)>[0@L18] new A}]

<Example: void main(java.lang.String[])>/temp$0 -> [NewObj{<Example: void main(java.lang.String[])>[0@L4] new A}]

<Example: void main(java.lang.String[])>/temp$1 -> [NewObj{<Example: void main(java.lang.String[])>[3@L5] new B}]

<Example: void main(java.lang.String[])>/temp$2 -> [NewObj{<B: A foo(A)>[0@L18] new A}]

<java.lang.Object: void <init>()>/%this -> [NewObj{<B: A foo(A)>[0@L18] new A}, NewObj{<Example: void main(java.lang.String[])>[0@L4] new A}, NewObj{<Example: void main(java.lang.String[])>[3@L5] new B}]

Points-to sets of all static fields

Points-to sets of all instance fields

Points-to sets of all array indexes

#reachable methods: 5

----------Reachable methods:----------

<A: void <init>()>

<B: A foo(A)>

<B: void <init>()>

<Example: void main(java.lang.String[])>

<java.lang.Object: void <init>()>

#call graph edges: 6

----------Call graph edges:----------

<A: void <init>()>[0@L10] invokespecial %this.<java.lang.Object: void <init>()>(); -> [<java.lang.Object: void <init>()>]

<B: A foo(A)>[1@L18] invokespecial temp$0.<A: void <init>()>(); -> [<A: void <init>()>]

<B: void <init>()>[0@L16] invokespecial %this.<A: void <init>()>(); -> [<A: void <init>()>]

<Example: void main(java.lang.String[])>[1@L4] invokespecial temp$0.<A: void <init>()>(); -> [<A: void <init>()>]

<Example: void main(java.lang.String[])>[4@L5] invokespecial temp$1.<B: void <init>()>(); -> [<B: void <init>()>]

<Example: void main(java.lang.String[])>[6@L6] temp$2 = invokevirtual b.<A: A foo(A)>(a); -> [<B: A foo(A)>]

----------------------------------------

In addition, Tai-e outputs the IRs for the classes of the program it analyzes to folder output/. The IRs are stored as .tir files which can be opened by general text editors.

We provide test driver pascal.taie.analysis.pta.CIPTATest for this assignment, and you could use it to test your implementation.

We encourage you to use your implementation of Assignment 4, i.e., CHA-based call graph builder, to analyze the test cases in this assignment (e.g., Example.java), and observe the precision differences on the resulting call graphs constructed by CHA and pointer analysis.

4 General Requirements

In this assignment, your only goal is correctness. Efficiency is not your concern.
DO NOT distribute the assignment package to any others.
Last but not least, DO NOT plagiarize. The work must be all your own!

5 Submission of Assignment

Your submission should be a zip file, which contains your implementation of

Solver.java

6 Grading

You can refer to Grade Your Programming Assignments to use our online judge to grade your completed assignments.

The points will be allocated for correctness. We will use your submission to analyze the given test files from the src/test/resources/ directory, as well as other tests of our own, and compare your output to that of our solution.

Good luck!

# Programming Assignment 5

A5: Context-Insensitive Pointer Analysis

# 1 Assignment Objectives

# 2 Implementing Pointer Analysis

# 2.1 Scope

# 2.2 New Rules

# 2.3 Tai-e Classes You Need to Know

# 2.4 Your Task [Important!]

# 3 Run and Test Your Implementation

# 4 General Requirements

# 5 Submission of Assignment

# 6 Grading

Programming Assignment 5

1 Assignment Objectives

2 Implementing Pointer Analysis

2.1 Scope

2.2 New Rules

2.3 Tai-e Classes You Need to Know

2.4 Your Task [Important!]

3 Run and Test Your Implementation

4 General Requirements

5 Submission of Assignment

6 Grading