Programming Assignment 1

A1: Live Variable Analysis and Iterative Solver

Course “Static Program Analysis” @Nanjing University

Assignments Designed by Tian Tan and Yue Li

1 Assignment Objectives

• Implement a live variable analysis for Java.
• Implement a generic iterative solver, which will be used to solve the data-flow problem you defined, i.e., the live variable analysis.

In this first programming assignment, you will implement a live variable analysis and an iterative solver on top of Tai-e. We have built a generic data-flow analysis framework in Tai-e, which provides analysis interfaces, necessary program information (e.g., control-flow graph), commonly used data structures (e.g., representation of data facts), etc., and thus you could easily write new data-flow analyses on top of it. In this assignment, you will implement the key parts of live variable analysis and iterative solver.

Note:

In this document (and the documents for other assignments), we only briefly explain some necessary APIs that are related to the assignments, and to learn how other related APIs work, or to get a more comprehensive understanding about the framework, you need to read the source code and the corresponding comments we provided. So please reserve some time for the source code reading and understanding, and this will help improve your ability for rapidly getting familiar with complicated programs.

Now, we suggest that you first setup the Tai-e project for Assignment 1 (in A1/tai-e/ of the assignment repo) by following Setup Tai-e Assignments.

2 Implementing Live Variable Analysis

2.1 Tai-e Classes You Need to Know

To implement live variable analysis on Tai-e, you need to know the following classes.

• pascal.taie.analysis.dataflow.analysis.DataflowAnalysis

  This is the interface between concrete data-flow analyses (e.g., live variable analysis and reaching definition) and data-flow analysis solver. It has 7 APIs, and in this assignment, you only need to focus on the first 5 APIs, which correspond to the five key elements in a data-flow analysis (page 297 of slides for Lecture 4), i.e., direction, boundary, initialization, meet operation and transfer function. All APIs of this class are commented in the source code, so that you could get familiar with them by reading the code and comments.

  The APIs in this class will be invoked by the data-flow analysis solver you write. Note that in our assignments, the transfer function manipulates statements, not basic blocks, which makes it simpler.

• pascal.taie.ir.exp.Exp

  This is one of the two key interfaces in Tai-e’s IR (another one, Stmt, will be introduced later), which represents all expressions in the program. This class has many subclasses, corresponding to various expressions. Here we show a tiny part of its class hierarchy: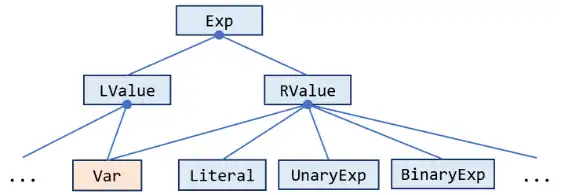

  

  In Tai-e’s IR, we classify all expressions as two kinds, LValue and RValue. LValue represents the expressions that can appear in the left-hand side of an assignment, i.e., variable (x = …;), field access (x.f = …;), and array access (x[i] = …;). Correspondingly, RValue represents the expressions at the right-hand side of assignments, such as literals (… = 1;) and binary expressions (… = a + b;). Note that some expressions can appear in both side of assignments, e.g., variables (represented by Var in Tai-e, as shown in the figure above). In this assignment, you only need to focus on the Var (of all expressions), as we are doing live variable analysis.

• pascal.taie.ir.stmt.Stmt

  This is another key interface in Tai-e’s IR, which represents all statements in the program. As each expression belongs to certain statement in a typical programming language, to implement live variable analysis, you need to obtain the variables that are defined and used in a statement. Stmt provides two convenient APIs for these two operations:

  • Optional<LValue> getDef()
  • List<RValue> getUses()

  Each Stmt can define at most one value and use zero or more values, and thus we use Optional and List to wrap the result of getDef() and getUses().

• pascal.taie.analysis.dataflow.fact.SetFact<Var>

  This class represents the data facts which can be seen as sets. For generality, SetFact is implemented as a generic class. It provides various set operations, e.g., add/remove elements, intersect/union with other sets, etc. You will use this class to represent the data facts in live variable analysis. Its APIs are commented in the source code, and you should read the source code and decide which APIs to use in this assignment.

• pascal.taie.analysis.dataflow.analysis.LiveVariableAnalysis

  This class implements DataflowAnalysis and defines live variable analysis. It is incomplete, and you need to finish it as explained in Section 2.2.

2.2 Your Task [Important!]

Your first task is to implement the following four APIs of LiveVariableAnalysis:

• SetFact newBoundaryFact(CFG)
• SetFact newInitialFact()
• void meetInto(SetFact,SetFact)
• boolean transferNode(Stmt,SetFact,SetFact)

which correspond to four parts of live variable analysis algorithm as shown below:

Here, the design of meetInto() might be a bit different from what you expect. It takes two facts as arguments (fact and target), and is supposed to meet fact into target. Unlike the equation in the above algorithm which sets OUT[B] to the union of IN facts of all successors of B, meetInto() meets the IN fact of each successor to OUT[B] individually, as illustrated by the following example.

We design meetInto() in this way for efficiency. Firstly, each call to meetInto() for the same control-flow confluence node manipulates the same SetFact object (as OUT fact of the node), thus we can avoid creating many new SetFact objects (for equation OUT[S] = U…, you may need to create multiple new temporary SetFact objects when computing the union of IN facts at each iteration for the same node). In addition, such design enables an optimization, i.e., we can avoid meeting unchanged facts. For example, in some iteration, IN[S2] changes and IN[S3] remains the same. Then unlike the big union equation in the lecture, we only need to meet IN[S2] into OUT[S1] and avoid meeting IN[S3]. This optimization is beyond the scope of this assignment, and you do not need to consider it in your implementation.

To support such meet strategy, you also need to give OUT[S] an initial fact (the same initial value as in IN[S]) for each statement.

Besides meetInto(), the other APIs to be implemented are straightforward. Note that the APIs of LiveVariableAnalysis are inherited from DataflowAnalysis, which is designed to support various analyses, thus you may not need to use all parameters of these APIs when you implement them in LiveVariableAnalysis.

We have provided code skeletons for all four APIs, and your task is to fill in the parts with comment “TODO – finish me”.

3 Implementing Iterative Solver

3.1 Tai-e Classes You Need to Know

To implement iterative solver on Tai-e, you need to know the following classes.

• pascal.taie.analysis.dataflow.fact.DataflowResult

  Each object of this class manages the facts of a CFG in a data-flow analysis. You could get/set IN/OUT facts of nodes in a CFG through its APIs.

• pascal.taie.analysis.graph.cfg.CFG

  This class represents control-flow graphs of the methods in a program. It is iterable, thus you could iterate the nodes of a CFG via a for loop:

  CFG<Node> cfg = ...;
  for (Node node : cfg) {
      ...
  }
  

  You could iterate predecessors/successors of a node by CFG.getPredsOf(Node) and CFG.getSuccsOf(Node), for example,

  for (Node succ : cfg.getSuccsOf(node)) {
      ...
  }
  

  For more information about CFG, please read its code and comments.

• pascal.taie.analysis.dataflow.solver.Solver

  This is the base class for data-flow analysis solvers. As there are different kinds of solvers, e.g., iterative solver and worklist solver (you will implement a worklist solver in the next assignment), we extract their common functionalities to this class. In run time, Tai-e builds CFGs and passes them to Solver.solve(CFG) to start the solver. You may notice that this class has two sets of initialize and doSolve methods, for supporting forward and backward data-flow analyses respectively (despite a bit redundant, such design will lead to a more clean and simpler code structure, and accordingly more straightforward implementation, compared with one analysis for two directions). This class is incomplete, and you need to finish it as explained in Section 3.2.

• pascal.taie.analysis.dataflow.solver.IterativeSolver

  This class extends Solver and implements iterative algorithm. It is incomplete too, and to be finished.

3.2 Your Task [Important!]

Your second task is to finish two APIs of the solver classes mentioned above:

• Solver.initializeBackward(CFG,DataflowResult)
• IterativeSolver.doSolveBackward(CFG,DataflowResult)

You only need to focus on backward-related methods as live variable analysis is a backward analysis. In initializeBackward(), you should implement the first three lines of the algorithm in Section 2.2. You should implement the while-loop of iterative algorithm in doSolveBackward().

Hint:

Each Solver holds an object of the corresponding data-flow analysis in its field analysis (LiveVariableAnalysis in this assignment), and you should use it to implement the solver.

4 Run and Test Your Implementation

You can run the analysis following the instructions described in document Set Up Tai-e Assignments. In this assignment, Tai-e performs live variable analysis for each method of input class, and outputs the analysis results, i.e., the data-flow information (live variables) in OUT fact of each statement:

--------------------<Assign: int assign(int,int,int)> (livevar)--------------------

[0@L4] d = a + b; null

[1@L5] b = d; null

[2@L6] c = a; null

[3@L7] return b; null

Each line starts with the position of the statement, e.g., [0@L4] means that the index of the statement in IR is 0, and it is in line 4 of the source code. Each line ends with the OUT fact of the statement, and it is null as you have not finished the analysis yet. After you implement the analysis, the output should be:

--------------------<Assign: int assign(int,int,int)> (livevar)--------------------

[0@L4] d = a + b; [a, d]

[1@L5] b = d; [a, b]

[2@L6] c = a; [b]

[3@L7] return b; []

In addition, Tai-e outputs the control-flow graphs of the methods it analyzes to folder output/. The CFGs are stored as .dot files, and can be visualized by Graphviz.

We provide test driver pascal.taie.analysis.dataflow.analysis.LiveVarTest for this assignment, and you could use it to test your implementation as described in Set Up Tai-e Assignments.

5 General Requirements

• In this assignment, your only goal is correctness. Efficiency is not your concern.

• DO NOT distribute the assignment package to any others.

• Last but not least, DO NOT plagiarize. The work must be all your own!

6 Submission of Assignment

Your submission should be a zip file, which contains your implementation of

• LiveVariableAnalysis.java
• Solver.java
• IterativeSolver.java

7 Grading

You can refer to Grade Your Programming Assignments to use our online judge to grade your completed assignments.

The points will be allocated for correctness. We will use your submission to analyze the given test files from the src/test/resources/ directory, as well as other tests of our own, and compare your output to that of our solution.

Good luck!