Tai-e

实验作业 1

作业 1：活跃变量分析和迭代求解器

南京大学《软件分析》课程
作业出品：谭添、李樾

1 作业导览

  • 为 Java 实现一个活跃变量分析（Live Variable Analysis）。
  • 实现一个通用的迭代求解器（Iterative Solver），用于求解数据流分析问题，也就是本次作业中的活跃变量分析。

我们已经在 Tai-e 的框架代码中提供了你需要的一切基础设施，包括但不限于：程序分析接口、常用数据结构（如数据流信息的表示）、必要的程序信息（如控制流图）等内容。由此，你就可以便利地在 Tai-e 上实现各类数据流分析了。例如在本次作业中，你要在框架代码中补全一些关键部分，从而实现要求的活跃变量分析与迭代求解器。

需要特别注意的是，所有作业文档都只会简要地介绍本次作业中必要的一些 API。因此，如果要搞清楚 API 的实现机制、真正理解框架代码，你必须留出时间阅读、理解相关类的源代码和相应的注释。这是你提升快速上手复杂代码能力的必经之路。

在阅读接下来的内容前，请先按照 Tai-e 框架（教学版）配置指南 将作业 1 对应的 Tai-e 项目（位于实验作业仓库的 A1/tai-e/ ）配置好。

2 实现活跃变量分析

2.1 Tai-e 中你需要了解的类

为了在 Tai-e 中实现活跃变量分析，你需要了解的类有：

  • pascal.taie.analysis.dataflow.analysis.DataflowAnalysis

    这是一个抽象的数据流分析类，是具体的数据流分析与求解器之间的接口。也就是说，一个具体的数据流分析（如活跃变量分析）需要实现它的接口，而求解器（如迭代求解器）需要通过它的接口来求解数据流。它共有七个 API，而在本次作业中，我们只关注与数据流分析相关的五个关键 API（见第 4 讲课件的第 297 页）：分析方向、边界条件、初始条件、meet 操作、transfer 函数。你可以阅读源代码与注释快速熟悉这些接口方法。

    需要注意的是，这里的API与课程中介绍的稍有区别：为了简单起见，这里的transfer函数处理的是单条语句而非程序块。

  • pascal.taie.ir.exp.Exp

    这是 Tai-e 的 IR 中的一个关键接口，用于表示程序中的所有表达式。它含有很多子类，对应各类具体的表达式。下面是一个 Exp 类继承结构的简单图示：

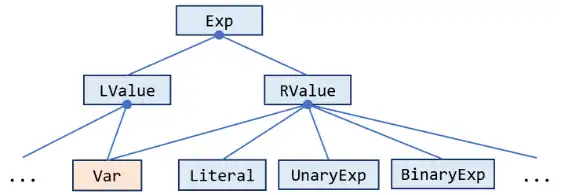
    Subclasses of Exp

    在 Tai-e 的 IR 中，我们把表达式分为两类：LValue 和 RValue。前者表示赋值语句左侧的表达式，如变量（x = … ）、字段访问（x.f = …）或数组访问（x[i] = …）；后者对应地表示赋值语句右侧的表达式，如数值字面量（… = 1;）或二元表达式（… = a + b;）。而有些表达式既可用于左值，也可用于右值，就比如变量（用Var类表示)。因为本次作业只进行活跃变量分析，所以你实际上只需要关注 Var 类就足够了。

  • pascal.taie.ir.stmt.Stmt

    这是 Tai-e 的 IR 中的另一个关键接口，它用于表示程序中的所有语句。对于一个典型的程序设计语言来说，每个表达式都属于某条特定的语句。为了实现活跃变量分析，你需要获得某条语句中定义或使用的所有表达式中的变量。Stmt 类贴心地为这两种操作提供了对应的接口：

    Optional<LValue> getDef()
List<RValue> getUses()

    每条 Stmt 至多只可能定义一个变量、而可能使用零或多个变量，因此我们使用 Optionalopen in new window 和 List 包装了 getDef() 和 getUses() 的结果。

  • pascal.taie.analysis.dataflow.fact.SetFact<Var>

    这个泛型类open in new window用于把 data fact 组织成一个集合。它提供了各种集合操作，如添加、删除元素，取交集、并集等。你同样需要阅读源码和注释来理解如何使用这个类表示活跃变量分析中的各种 data fact。

  • pascal.taie.analysis.dataflow.analysis.LiveVariableAnalysis

    这个类通过实现 DataflowAnalysis 的接口来定义具体的活跃变量分析。你需要按照第 2.2 节中的说明补全这个类。

2.2 你的任务 [重点!]

你的第一个任务是实现 LiveVariableAnalysis 中的如下 API：

  • SetFact newBoundaryFact(CFG)
  • SetFact newInitialFact()
  • void meetInto(SetFact,SetFact)
  • boolean transferNode(Stmt,SetFact,SetFact)

这些 API 对应下图算法中的四个部分：

Iterative Algorithm

此处 meetInto() 的设计可能与你设想的稍有差别：它接受 fact 和 target 两个参数并把 fact 集合并入 target 集合。这个函数有什么用呢？考虑一下上图中 meetInto() 附近的那行伪代码，它会取出 B 的所有后继，然后把它们 IN facts 的并集赋给 OUT[B]。如果这行代码用 meetInto() 来实现，那么我们就可以根据下图所示，用 meetInto(IN[S], OUT[B]) 把 B 的每个后继 S 的 IN fact 直接并入到 OUT[B] 中：

MeetInto Example

这样设计 meetInto() 是出于效率考量。首先，在一个控制流合并节点多次调用 meetInto() 时，我们都在改写同一个对象。这样，我们可以避免像伪代码 OUT[S] = U… 所描述的那样，每次合并两个集合就会创建出一个新的 SetFact 对象保存结果。此外，这种设计还有更多的优化空间：我们可以忽略一些不变的 IN fact 来提高效率。例如在某次迭代中，如果 IN[S2] 有改变而 IN[S3] 没有，我们就不必依照课堂上讲述的办法求出 IN[S2] 和 IN[S3] 的并，而大可以忽略 IN[S3]，只把 IN[S2] 并入 OUT[S1]。不过这个优化超出了本次作业的范畴，你不用考虑实现它。

当然，为了实现上面所说的 meet 策略，你需要在初始化阶段给每条语句的 OUT[S] 赋上和 IN[S] 一样的初值。

除了 meetInto() ，其他 API 的实现都直接依照了课上讲述的算法。需要注意的是，框架中LiveVariableAnalysis 的 API 都继承自 DataflowAnalysis，而该类为了支持各种数据流分析，接口中可能包含了一些你用不上的参数。因此，某些参数在作业中用不上是正常现象。

我们已经提供了四个 API 的框架代码，你的任务就是补全标有“TODO – finish me”的部分。

3 实现迭代求解器

3.1 Tai-e 中你需要了解的类

为了在 Tai-e 中实现迭代求解器，你需要了解的类有：

  • pascal.taie.analysis.dataflow.fact.DataflowResult

    该类对象用于维护数据流分析的 CFG 中的 fact。你可以通过它的 API 获取、设置 CFG 节点的 IN facts 和 OUT facts。

  • pascal.taie.analysis.graph.cfg.CFG

    这个类用于表示程序中方法的控制流图（control-flow graphs）。它是可迭代的，也就是说你可以通过一个 for 循环遍历其中的所有节点：

    CFG<Node> cfg = ...;
for (Node node : cfg) {
    ...
}

    你可以通过 CFG.getPredsOf(Node) 和 CFG.getSuccsOf(Node) 这两个方法遍历 CFG 中节点的所有前驱和后继，比如你可以写：

    for (Node succ : cfg.getSuccsOf(node)) {
    ...
}

    再次强调：请通过阅读源码和注释来获得更多关于CFG类的信息。

  • pascal.taie.analysis.dataflow.solver.Solver

    这是数据流分析求解器的基类，包含了求解器的抽象功能。本次作业要实现的迭代求解器就是它的一个派生类（下次作业中的 worklist 求解器也是）。Tai-e 会构建待分析程序的 CFG 并传给 Solver.solve(CFG)，然后世界就开始运转了。你可能注意到了，这个类中有两组 initialize 和 doSolve 方法，分别用于处理前向和后向的数据流分析。虽然稍显冗余，但在这样的设计下代码结构会更干净、直接一些。这个类也是需要你补全实现的，这在第 3.2 节中进一步解释。

  • pascal.taie.analysis.dataflow.solver.IterativeSolver

    这个类扩展了 Solver 的功能并实现了迭代求解算法。当然，它也有待你补全。

3.2 你的任务 [重点!]

你的第二个任务是实现上面提到的 Solver 类的两个方法：

  • Solver.initializeBackward(CFG,DataflowResult)
  • IterativeSolver.doSolveBackward(CFG,DataflowResult)

因为活跃变量分析是一个后向分析，所以你只需要关注后向分析相关的方法就足够了。在 initializeBackward() 中，你需要实现第 2.2 节中算法的前三行；在 doSolveBackward() 则要完成对应的 while 循环。

提示：

每个 Solver 对象都在字段 analysis 中保存了相应的数据流分析对象，在本次作业中就是一个 LiveVariableAnalysis 对象。你需要用它提供的相关接口来实现分析求解器。

4 运行与测试

你可以按我们在 Tai-e 框架（教学版）配置指南 中提到的方式来运行你的分析。在本作业中，Tai-e 对输入类的每个方法进行活跃变量分析，并输出分析的结果，也就是每个语句的 OUT fact 所包含的数据流信息（活跃变量）：

--------------------<Assign: int assign(int,int,int)> (livevar)--------------------
[0@L4] d = a + b; null
[1@L5] b = d; null
[2@L6] c = a; null
[3@L7] return b; null

输出结果的每一行以该语句的位置信息开始，例如 [0@L4] 表示该语句在 IR 中的索引为 0，且在源码中处于第 4 行。输出结果的每一行末尾为该语句的 OUT fact，（当你未完成作业时结果为 null）。当你完成了所有的空缺代码后，分析的输出应当形如：

--------------------<Assign: int assign(int,int,int)> (livevar)--------------------
[0@L4] d = a + b; [a, d]
[1@L5] b = d; [a, b]
[2@L6] c = a; [b]
[3@L7] return b; []

此外，Tai-e 将被分析方法的控制流图输出到 output/ 文件夹，它们被存储为 .dot 文件，你可以用可视化工具 Graphvizopen in new window 来查看这些控制流图。

我们为本次作业提供了测试驱动类 pascal.taie.analysis.dataflow.analysis.LiveVarTest，你可以按照 Tai-e 框架（教学版）配置指南 中描述的方式来测试你的实现是否正确。

5 通用准则

  • 在这次作业中，你只需要保证实现的正确性。不必过早考虑效率。

  • 禁止把你的作业包发给其他人参考。

  • 禁止抄袭。自己的工作必须由自己完成。

6 作业提交

你应当提交一个 zip 文件，其中包括你实现好的以下类：

  • LiveVariableAnalysis.java
  • Solver.java
  • IterativeSolver.java

7 评分

你可以参照 实验作业评测系统使用指南 来使用我们的作业评测系统对你完成的作业进行评分。

你的分数将取决于你实现的正确性：我们会用你提交的实现来分析 src/test/resources/ 目录下的测试用例和另外一些未公开的测试用例，然后将得到的结果与标准实现的分析结果比较，从而进行评分。

祝君好运！

Last Updated: