作业 4：类层次结构分析与过程间常量传播

南京大学《软件分析》课程

作业出品：谭添、李樾

1 作业导览

为 Java 实现一个类层次结构分析（Class Hierarchy Analysis，CHA）。
实现过程间常量传播。
实现过程间数据流传播的 worklist 求解器。

在本次实验作业中，你将在 Tai-e 的基础之上为 Java 实现一个基于类层次结构（下面简称为 CHA）的调用图（call graph）构造器。接着为了展现它的用处，你需要依靠你实现的调用图实现一个过程间常量传播分析。此外，为了使得你的过程间常量传播能够正常运行，你还需要实现一个 worklist 求解器来支持过程间数据流分析（虽然在软件分析课程中，我们并没有教过你实现过程间分析的具体方法，但是不必担心，通过本次作业，你会掌握相关的知识和实现方法）。

本次作业的分析范围和第二次作业是一致的，也就是说你仍然只需要考虑针对 int 类型变量的常量传播，只不过在本次作业中，你需要更准确地处理方法调用。如果你的实现是正确的，那么在实验的最后你就可以发现：与保守处理方法调用的过程内常量传播相比，过程间常量传播可以达到更好的精度。

在阅读接下来的内容前，请先按照 Tai-e 框架（教学版）配置指南将作业 4 对应的 Tai-e 项目（位于实验作业仓库的 A4/tai-e/ ）配置好。

2 实现类层次结构分析（CHA）

在本次作业中，你需要处理 Java 语言的四种方法调用：invokestatic、invokespecial、invokeinterface 和 invokevirtual（已经在第 7 讲介绍过了哦）。当然，Java 中的一些新特性会让方法调用的情形更复杂：比如 Java 8 开始允许接口定义非抽象方法（default methodsopen in new window）；还有从 Java 11 开始，invokeinterface 和 invoke-virtual 可以调用 private 方法了。这都会使我们构建调用图的过程变得更复杂。而简单起见，你并不需要在本次作业中处理这些改动。

2.1 Tai-e 中你需要了解的类

本次作业中，有一些类包含了很多 API。为了减轻你的压力，我们将会介绍一些你可能会用到的相关的类和 API。我们将以自顶到下的方式来介绍这些类，也就是说，我们会首先介绍构建调用图的关键类（DefaultCallGraph），紧接着介绍与它相关的其他类。

pascal.taie.analysis.graph.callgraph.DefaultCallGraph
该类代表了程序的调用图。它提供了多样的 API（继承自类 AbstractCallGraph）来获取到调用图的信息。另外，它还提供了一些修改调用图的 API，你可以借此来建立调用图。
- Stream<Invoke> callSitesIn(JMethod)：返回给定方法 JMethod 中的所有 call sites。
- boolean contains(JMethod): 返回当前调用图是否含有给定的方法，即给定方法 JMethod 在当前调用图中是否可达。
- boolean addReachableMethod(JMethod): 向当前调用图中添加方法 JMethod 并将方法标记成可达的。
- boolean addEdge(Edge<Invoke,JMethod>): 向当前调用图中添加一条调用边。
pascal.taie.analysis.graph.callgraph.CallKind
该枚举类型表示调用图中边的种类，包括 INTERFACE、VIRTUAL、SPECIAL 和 STATIC，它对应第 7 讲中介绍过的 Java 的四种调用类型（call kind）。
pascal.taie.analysis.graph.callgraph.Edge<Invoke,JMethod>
该类表示调用图中的边。每一条边从调用点（call site，Tai-e 中为 Invoke 类型）出发，指向被调用方法（callee method，类型为 JMethod）。在创建一条边的时候，你需要向构造方法提供调用类型、调用点和被调用方法的信息。
pascal.taie.ir.stmt.Invoke (subclass of Stmt)
该类表示程序中的方法调用（举个例子：x = o.m(a1,a2,…)）以及调用图中的调用点。它提供了一些 API 来获取调用点的各种信息。明确一点：你需要使用 getMethodRef() 来获取目标方法的签名信息。
pascal.taie.ir.proginfo.MethodRef
Tai-e 中的目标方法引用，如调用点的目标方法。它包含了调用点所调用的目标方法的签名信息。
- JClass getDeclaringClass()：返回该方法签名的声明类，即声明该方法的类。（也就是第 7 讲课件的第 24 页中所描述的 class type）；
- Subsignature getSubsignature()：返回被调用方法的子签名（subsignature）。稍后我们回来介绍子签名类——Subsignature。
对 MethodRef，在本次作业中你只需要使用上面提到的两个 API。
pascal.taie.language.classes.JMethod
该类表示 Tai-e 中的 Java 方法。每个 JMethod 的实例关联着一个方法并包含该方法的各种信息。
- boolean isAbstract(): 如果该 JMethod 是一个没有方法体的抽象方法，则返回 true，否则返回 false；
pascal.taie.language.classes.JClass
该类表示 Tai-e 中的 Java 类。每个 JClass 的实例关联着一个类并包含该类的各种信息。
- JClass getSuperClass(): 返回该类的父类。如果这个类在类层次结构的顶端（没有父类），比如 java.lang.Object，则返回 null。
- JMethod getDeclaredMethod(Subsignature): 根据子签名返回该类中声明的对应方法。如果该类中没有该子签名对应的方法，则返回 null。
- boolean isInterface(): 返回该类是否是一个接口。
pascal.taie.language.classes.Subsignature
该类表示 Tai-e 中的子签名。一个方法的子签名只包含它的方法名和方法签名的描述符（在第 7 讲课件的第 24 页有所介绍）。举个例子，下面方法 foo 的子签名是：“T foo(P,Q,R)” ，而它的完整签名是：“<C: T foo(P,Q,R)>”。
```
class C {
    T foo(P p, Q q, R r) { … }
}
```
pascal.taie.language.classes.ClassHierarchy
该类提供了类层次结构的相关信息。
- Collection<JClass> getDirectSubclassesOf(JClass): 对于给定类，返回直接继承该类的子类。
- Collection<JClass> getDirectSubinterfacesOf(JClass): 对于一个给定接口，返回直接继承该接口的子接口。
- Collection<JClass> getDirectImplementorsOf(JClass): 对于一个给定接口，返回直接实现了该接口的类。
举个例子，在下面的 class hierarchy 中，I, II, III 是接口，其他均为类：
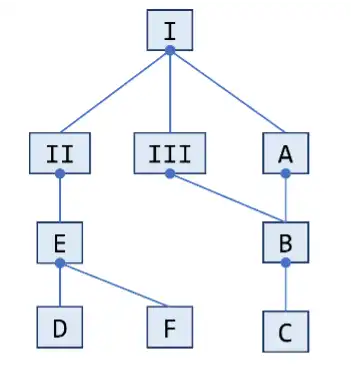
那么
- getDirectSubclassesOf(A) = [B]
- getDirectSubinterfacesOf(I) = [II, III]
- getDirectImplementorsOf(II) = [E]
pascal.taie.analysis.graph.callgraph.CHABuilder
这个类通过 CHA 来建立调用图。目前该类是不完整的，你将会在第 2.2 节的讲解和帮助下完成它。

2.2 你的任务 [重点!]

你的第一个任务是完成 CHABuilder 类。你需要完成以下三个 API：

JMethod dispatch(JClass,Subsignature)
该方法实现了第 7 讲课件的第 26 页中描述的 Dispatch 方法。特别地，如果找不到满足要求的方法，返回 null。
Set<JMethod> resolve(Invoke)
该方法实现了第 7 讲课件的第 33 页中描述的 Resolve 方法。
提示：
你可以使用 CallGraphs.getCallKind(Invoke) 来获得调用点的调用类型。
CallGraph<Invoke, JMethod> buildCallGraph(JMethod)
该方法实现了第 7 讲课件的第 52 页描述的 BuildCallGraph 算法。

我们提供了上述 3 个 API 的代码框架。你的任务是填写所有标有注释 “TODO – finish me” 的部分。

3 实现过程间常量传播

3.1 Edge Transfer

过程间常量传播和过程内常量传播很像。它们的主要区别是：过程间常量传播使用了 edge transfer，因此能够更准确地处理方法调用和返回所产生的过程间数据流。

举一个前向分析的例子，在传统的过程内数据流分析中，如果我们想计算一个节点的IN fact，我们可以直接meet该节点的全部前驱的OUT fact：

$IN [B] = ⋃_{P a predecessor of B} OUT [P]$

然而，在过程间数据流分析中，为了计算一个节点的 IN fact，我们需要先对该节点的前驱的 OUT fact 应用 edge transfer，然后把得到结果 meet 进该节点的 IN fact。

举个例子，这是第 7 讲中出现过的一个 ICFG：

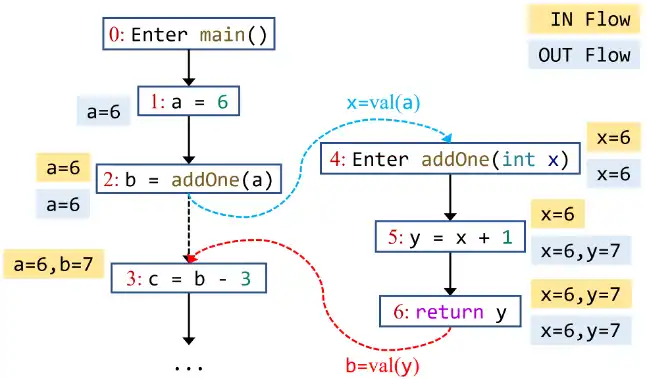
为了计算第 4 条语句的 IN fact，也就是方法 addOne() 的 entry 节点的 IN fact，我们需要对 2→4 这条边应用 edge transfer，这样使得第 2 条语句的 OUT fact（a=6）转换为 x=6，并最终 meet 结果 x=6 到第四条语句的 IN fact中。

我们定义了 transferEdge(edge, fact) 函数来实现 edge transfer。它以 ICFG 中的一条边（对应参数 edge）和边的源节点的 OUT fact（对应参数fact）为输入，并输出经transfer计算之后的结果fact。据此，我们把计算IN fact的转换函数调整为：

$IN [B] = ⋃_{P a predecessor of B} t r a n s f e r E d g e (P \to B, OUT [P])$

我们曾在第 7 讲中提到过，在过程间常量传播中，transfer edge 需要处理的边被分为以下四种：

Normal edge: 这种边一般是与过程间调用无关的边，edge transfer 函数不需要对此进行特殊的处理。这种边上的 fact 经 transfer edge 之后不会有任何改变。换句话说，此时 edge transfer 是一个恒等函数，即 transferEdge(edge, fact) = fact。
Call-to-return edge: 对于方法调用 x = m(…)，edge transfer 函数会把等号左侧的变量（在这个例子里也就是 x）和它的值从 fact 中kill 掉。而对于等号左侧没有变量的调用，比如 m(…)，edge transfer 函数的处理方式与对待 normal edge 的一致：不修改 fact，edge transfer 是一个恒等函数。
Call edge: 对于这种边，edge transfer 函数会将实参（argument）在调用点中的值传递给被调用函数的形参（parameter）。具体来说，edge transfer 首先从调用点的 OUT fact 中获取实参的值，然后返回一个新的 fact，这个 fact 把形参映射到它对应的实参的值。举个例子，在图 1 里，transferEdge(2→4, {a=6}) = {x=6}。此时，edge transfer 函数的返回值应该仅包含被调用函数的形参的值（比如图 1 里，addOne() 的 x）。
Return edge: edge transfer 函数将被调用方法的返回值传递给调用点等号左侧的变量。具体来说，它从被调用方法的 exit 节点的 OUT fact 中获取返回值（可能有多个，你需要思考一下该怎么处理），然后返回一个将调用点等号左侧的变量映射到返回值的 fact。举个例子，在图1中，transferEdge(6→3, {x=6,y=7}) = {b=7}。此时，edge transfer 函数返回的结果应该仅包含调用点等号左侧变量的值（例如图1在第三条语句处的b）。如果该调用点等号左侧没有变量，那么 edge transfer 函数仅会返回一个空 fact。

在接下来的章节，我们将会向你介绍更多关于如何在 Tai-e 中实现上述这些 edge transfer 函数的信息。

3.2 Tai-e 中你需要了解的类

pascal.taie.analysis.graph.icfg.ICFGEdge
该类是一个抽象类，它表示了 ICFG 中的边。而它有四个子类，分别关联着上一节中提到的四种 ICFG 边：Normal Edge、CallToReturnEdge、CallEdge、ReturnEdge：
- pascal.taie.analysis.graph.icfg.NormalEdge
- pascal.taie.analysis.graph.icfg.CallToReturnEdge
- pascal.taie.analysis.graph.icfg.CallEdge
- pascal.taie.analysis.graph.icfg.ReturnEdge
这些类都非常简单易懂并且有详尽的注释，请好好阅读源码来认识它们吧。
pascal.taie.analysis.dataflow.inter.InterDataflowAnalysis
这是一个过程间数据流分析的接口。它总共有 6 个API。它的前 5 个 API 都与过程内数据流分析 DataflowAnalysis 的相同，所以如果需要，你可以翻看此前的作业手册再次认识它们。而它的最后一个 API 就是 transferEdge()，也就是我们在第 3.1 节中介绍的 edge transfer 函数。这 6 个 API将被过程间数据流分析的求解器调用，而你的任务就是利用这些 API 实现这个求解器。
pascal.taie.analysis.dataflow.inter.AbstractInterDataflowAnalysis
该抽象类实现了 InterDataflowAnalysis，并为 InterDataflowAnalysis 的实现提供了一些基本的功能。说得明白一点，它把 ICFG 中不同的点和边分派给对应 transfer 方法。这样一来，我们的分析的实现就可以分别处理各类的点和边。
pascal.taie.analysis.dataflow.inter.InterConstantPropagation
该类继承自 AbstractInterDataflowAnalysis，并且定义了过程间常量传播。但是它还是不完整的。你需要根据第 3.3 节的描述完成它。
pascal.taie.ir.exp.InvokeExp
该类表示程序中的方法调用表达式。它包含了被调用的方法引用和传入的各个参数。具体的细节和如何使用，需要你阅读源码和相关注释来了解。

3.3 你的任务 [重点!]

你的第二个任务是完成 InterConstantPropagation 的这些 API：

boolean transferCallNode(Stmt,CPFact,CPFact)
boolean transferNonCallNode(Stmt,CPFact,CPFact)
CPFact transferNormalEdge(NormalEdge,CPFact)
CPFact transferCallToReturnEdge(CallToReturnEdge,CPFact)
CPFact transferCallEdge(LocalEdge,CPFact)
CPFact transferReturnEdge(LocalEdge,CPFact)

InterConstantPropagation 类包含了一个 ConstantPropagation 类的字段：cp，这使得你可以利用过程内常量传播实现的逻辑。但是ConstantPropagation.java 目前还和以前一样没有实现完全，所以，为了防止你的过程间常量分析罢工，你首先需要补全 ConstantPropagation.java。你可以从你此前已经完成的作业中复制代码，并粘贴到本次作业中。注意，在提交作业的时候，你不必提交 ConstantPropagation.java，这样就算你之前作业中的常量传播分析的实现有问题，它也不会影响影响你本次作业的得分。

提示：

你在实现 transfer*Edge() 方法的时候，不应该修改第二个参数，也就是该边的源节点的 OUT fact。
我们在第二次作业中介绍过，你可以从 IR 类中获取方法的参数，且可以使用 API JMethod.getIR() 来获取一个方法的 IR。

4 实现过程间 Worklist 求解器

4.1 算法

过程间 worklist 求解器所使用的算法和你在第二次作业中实现的过程内worklist求解器的算法大体上是一样的。它们仅有两处不同：

在第 3.1 节介绍过，在计算一个节点的 IN fact 时，过程间求解器需要对传入的 edge 和前驱们的 OUT facts 应用 edge transfer 函数（transferEdge）。
在初始化的过程中，过程间求解器需要初始化程序中所有的 IN/OUT fact，也就是 ICFG 的全部节点。但你仅需要对 ICFG 的 entry 方法（比如 main 方法）的 entry 节点设置 boundary fact。这意味着其他方法的 entry 节点和非 entry 节点的初始 fact 是一样的。

4.2 Tai-e 中你需要了解的类

pascal.taie.analysis.dataflow.fact.DataflowResult
你已经在此前的作业中见过这个类了。在本次作业中，你将会使用一个 DataflowResult 对象来管理 ICFG 中所有节点的 fact。通过使用该类中的 API，你可以获取或设置 ICFG 中各个节点的 IN/OUT fact。
pascal.taie.analysis.graph.icfg.ICFG
该类代表的是程序的过程间控制流图。与 CFG 相似，它也是可迭代的（iterable），所以你可以利用 for 循环来迭代 ICFG 的所有节点：
```
ICFG icfg = ...;
for (Node node : icfg) {
    ...
}
```
关于 ICFG 的更多信息，请阅读源码和有关注释。
pascal.taie.analysis.dataflow.inter.InterSolver
该类是过程间数据流分析的求解器。它目前是不完整的，需要你根据第 4.3 节的说明来完成它。

4.3 你的任务 [重点!]

终于，这是你最后的任务了——完成 InterSolver 的两个 API：

void initialize()
void doSolve()

同样，你只需要实现前向分析的求解器，因为过程间常量分析就是前向的。你需要在 initialize() 中初始化 ICFG 节点的 IN/OUT fact，还需要在 doSolve() 中实现 worklist 算法的主要部分。

提示：

我们已经为待求解的分析、程序的 ICFG 和管理 fact 的 DataflowResult 创建了对象，并且把它们分别存在了 InterSolver 类的 analysis、icfg 和 result 字段里。这样，你可以很轻易地访问和操作这些对象。

5 运行与测试

你可以用 Tai-e 框架（教学版）配置指南中介绍的方法来运行分析算法。本次作业中，Tai-e 首先运行 CHA 来创建程序的调用图，然后根据调用图构建 ICFG，最后在 ICFG 上运行过程间常量传播分析。为了方便调试，Tai-e 会将 CHA 和过程间常量分析的结果都输出到控制台。

#reachable methods: 0

----------Reachable methods:----------

#call graph edges: 0

----------Call graph edges:----------

----------------------------------------

--------------------<Example: void <init>()> (inter-constprop)--------------------

[0@L1] invokespecial %this.<java.lang.Object: void <init>()>(); null

[1@L1] return; null

--------------------<Example: void main(java.lang.String[])> (inter-constprop)--------------------

[0@L5] a = 6; null

[1@L6] temp$1 = invokestatic <Example: int addOne(int)>(a); null

[2@L6] b = temp$1; null

[3@L7] %intconst0 = 3; null

[4@L7] c = b - %intconst0; null

[5@L8] temp$3 = invokestatic <Example: int ten()>(); null

[6@L8] b = temp$3; null

[7@L9] c = a * b; null

[8@L9] return; null

--------------------<Example: int addOne(int)> (inter-constprop)--------------------

[0@L13] %intconst0 = 1; null

[1@L13] y = x + %intconst0; null

[2@L14] return y; null

--------------------<Example: int ten()> (inter-constprop)--------------------

[0@L17] temp$0 = 10; null

[1@L18] return temp$0; null

上面的例子已经在第 7 讲中介绍过。因为当前你还没有实现作业要求完成分析，所以此时该分析的调用图为空（没有任何的可达方法）并且 OUT fact 均为 null。

而当你完成了这些分析之后，输出应当形如：

#reachable methods: 3

----------Reachable methods:----------

<Example: int addOne(int)>

<Example: int ten()>

<Example: void main(java.lang.String[])>

#call graph edges: 2

----------Call graph edges:----------

<Example: void main(java.lang.String[])>[1@L6] temp$1 = invokestatic <Example: int addOne(int)>(a); -> [<Example: int addOne(int)>]

<Example: void main(java.lang.String[])>[5@L8] temp$3 = invokestatic <Example: int ten()>(); -> [<Example: int ten()>]

----------------------------------------

--------------------<Example: void main(java.lang.String[])> (inter-constprop)--------------------

[0@L5] a = 6; {a=6}

[1@L6] temp$1 = invokestatic <Example: int addOne(int)>(a); {a=6}

[2@L6] b = temp$1; {a=6, b=7, temp$1=7}

[3@L7] %intconst0 = 3; {%intconst0=3, a=6, b=7, temp$1=7}

[4@L7] c = b - %intconst0; {%intconst0=3, a=6, b=7, c=4, temp$1=7}

[5@L8] temp$3 = invokestatic <Example: int ten()>(); {%intconst0=3, a=6, b=7, c=4, temp$1=7}

[6@L8] b = temp$3; {%intconst0=3, a=6, b=10, c=4, temp$1=7, temp$3=10}

[7@L9] c = a * b; {%intconst0=3, a=6, b=10, c=60, temp$1=7, temp$3=10}

[8@L9] return; {%intconst0=3, a=6, b=10, c=60, temp$1=7, temp$3=10}

--------------------<Example: int addOne(int)> (inter-constprop)--------------------

[0@L13] %intconst0 = 1; {%intconst0=1, x=6}

[1@L13] y = x + %intconst0; {%intconst0=1, x=6, y=7}

[2@L14] return y; {%intconst0=1, x=6, y=7}

--------------------<Example: int ten()> (inter-constprop)--------------------

[0@L17] temp$0 = 10; {temp$0=10}

[1@L18] return temp$0; {temp$0=10}

另外，Tai-e 会将它所分析程序的 ICFG 输出到目录 output/ 下。ICFG 被保存为可以使用 Graphviz 可视化的 .dot 格式。注意，每个 ICFG 都是基于一个调用图构建的，所以一旦你修改了 CHABuilder，那么即使分析同一个程序，Tai-e 也可能会输出不同的 ICFG。

我们已经提供了 pascal.taie.analysis.graph.callgraph.cha.CHATest 和 pascal.taie.analysis.dataflow.analysis.constprop.InterCPTest 作为 CHA 和过程间常量传播的测试驱动类。如 Tai-e 框架（教学版）配置指南所介绍，你可以使用它们来测试你代码的正确性。

我们非常鼓励你使用你此前在第二次作业中的实现（即过程内常量传播）来分析本次作业中的测试用例，并观察过程间分析和过程内分析的精度差异。

在本次作业中，你实现的分析是过程间分析。过程间分析会从入口方法来分析整个程序，也就是 main 方法。所以，如果你想要为你实现写一些测试用例，请确保被分析的类有一个 main 方法：public static void main(String[])。

6 通用准则

在这次作业中，你只需要保证实现的正确性。不必过早考虑效率。
禁止把你的作业包发给其他人参考。
禁止抄袭。自己的工作必须由自己完成。

7 作业提交

你提交的内容应当是一个 zip 压缩包文件，其中包括你的代码文件：

CHABuilder.java
InterConstantPropagation.java
InterSolver.java

8 评分

你可以参照实验作业评测系统使用指南来使用我们的作业评测系统对你完成的作业进行评分。

你的分数将取决于你实现的正确性：我们会用你提交的实现来分析 src/test/resources/ 目录下的测试用例和另外一些未公开的测试用例，然后将得到的结果与标准实现的分析结果进行比较，从而进行评分。

祝君好运！

作业 4：类层次结构分析与过程间常量传播

# 1 作业导览

# 2 实现类层次结构分析（CHA）

# 2.1 Tai-e 中你需要了解的类

# 2.2 你的任务 [重点!]

# 3 实现过程间常量传播

# 3.1 Edge Transfer

# 3.2 Tai-e 中你需要了解的类

# 3.3 你的任务 [重点!]

# 4 实现过程间 Worklist 求解器

# 4.1 算法

# 4.2 Tai-e 中你需要了解的类

# 4.3 你的任务 [重点!]

# 5 运行与测试

# 6 通用准则

# 7 作业提交

# 8 评分

1 作业导览

2 实现类层次结构分析（CHA）

2.1 Tai-e 中你需要了解的类

2.2 你的任务 [重点!]

3 实现过程间常量传播

3.1 Edge Transfer

3.2 Tai-e 中你需要了解的类

3.3 你的任务 [重点!]

4 实现过程间 Worklist 求解器

4.1 算法

4.2 Tai-e 中你需要了解的类

4.3 你的任务 [重点!]

5 运行与测试

6 通用准则

7 作业提交

8 评分