Programming Assignment 4

A4: CHA and Interprocedural Constant Propagation

Course “Static Program Analysis” @Nanjing University

Assignments Designed by Tian Tan and Yue Li

1 Assignment Objectives

Implement a class hierarchy analysis (CHA) for Java.
Implement an interprocedural constant propagation.
Implement a worklist solver for interprocedural data-flow analysis.

In this programming assignment, you will implement a CHA-based call graph builder for Java on top of Tai-e. To demonstrate the usefulness of call graph, you will complete an interprocedural constant propagation, which uses the call graph constructed by your analysis. To make interprocedural constant propagation work, you also need to implement a worklist solver that supports interprocedural data-flow analysis (In the lecture, we did not teach you how to implement interprocedural analysis in detail. Don’t worry, you will learn it from this assignment).

The scope of this assignment is the same as in Assignment 2, i.e., you still only need to focus on constant propagation for int values, and the only difference is that you will handle method calls more precisely in this assignment. If your implementation is correct, you can observe that interprocedural constant propagation achieves better precision than intraprocedural counterpart which treats method calls conservatively.

Now, we suggest that you first setup the Tai-e project for Assignment 4 (in A4/tai-e/ of the assignment repo) by following Setup Tai-e Assignments.

2 Implementing Class Hierarchy Analysis

In this assignment, you will deal with four kinds of method invocations in Java, i.e., invokestatic, invokespecial, invokeinterface, and invokevirtual as explained in Lecture 7. Note that since Java 8, interfaces can also declare non-abstract methods (default methodsopen in new window) and since Java 11, invokeinterface and invoke-virtual can call private methods. These new changes complicate the call graph construction. For simplicity, you are not required to handle them in this assignment.

2.1 Tai-e Classes You Need to Know

Some classes used in this assignment have many APIs, thus, to save your effort, we will introduce the APIs of these classes that you may use. Below we present the classes in a top-down manner, i.e., we first introduce the key class of call graph construction (DefaultCallGraph), and then the other classes it depends on.

pascal.taie.analysis.graph.callgraph.DefaultCallGraph
This class represents call graph of the program. It provides various APIs (inherited from class AbstractCallGraph) to obtain the information of the call graph, and the APIs to modify the call graph, which you may use to build the call graph.
- Stream<Invoke> callSitesIn(JMethod): returns all call sites in the given method.
- boolean contains(JMethod): returns whether the call graph contains the given method, i.e., the method is reachable in this call graph.
- boolean addReachableMethod(JMethod): adds a method to this call graph. After this call, the method becomes reachable in the call graph.
- boolean addEdge(Edge<Invoke,JMethod>): adds a call edge to this call graph.
pascal.taie.analysis.graph.callgraph.CallKind
This enumeration type represents the kinds of call graph edges. It defines several constants including INTERFACE, VIRTUAL, SPECIAL and STATIC, corresponding to four kinds of invocations in Java we introduced in Lecture 7.
pascal.taie.analysis.graph.callgraph.Edge<Invoke,JMethod>
This class represents call graph edges. Each edge connects a call site (of type Invoke) to a callee method (of type JMethod). To construct an Edge, you need to provide the CallKind, a call site and a callee method to its constructor.
pascal.taie.ir.stmt.Invoke (subclass of Stmt)
This class represents method calls, e.g., x = o.m(a1,a2,…), in the program, and also the call sites in the call graph. It provides APIs to obtain various information of the call site. Specifically, you will use getMethodRef() to obtain signature information of the target methods.
pascal.taie.ir.proginfo.MethodRef
Tai-e’s representation to a reference to target method(s) as it appears in a call site. It contains the signature information of the target methods of the call site.
- JClass getDeclaringClass(): returns the declaring class of the method signature (corresponding to class type in page 24 of Lecture 7).
- Subsignature getSubsignature(): returns the subsignature of the callee method(s). We will introduce class Subsignature later.
For MethodRef, you should only use the above two APIs in this assignment.
pascal.taie.language.classes.JMethod
Tai-e’s representation of Java methods. Each instance of JMethod corresponds to a method in the program and contains various information about the method.
- boolean isAbstract(): if this JMethod is an abstract method that has no method body, then it returns true; otherwise, it returns false.
pascal.taie.language.classes.JClass
Tai-e’s representation of Java classes. Each instance of JClass corresponds to a class in the program and contains various information about the class.
- JClass getSuperClass(): returns the superclass of this class. If this class is the top of class hierarchy, i.e., java.lang.Object, null is returned.
- JMethod getDeclaredMethod(Subsignature): returns the method declared in this class with the given subsignature. If no method with the given subsignature can be found, null is returned.
- boolean isInterface(): returns whether this class is an interface.
pascal.taie.language.classes.Subsignature
Tai-e’s representation of subsignature. The subsignature of a method only contains the method name and the descriptor of a method signature as introduced in page 24 of Lecture 7. For example, the subsignature of the following method foo is “T foo(P,Q,R)” while its signature is “<C: T foo(P,Q,R)>”.
```
class C {
    T foo(P p, Q q, R r) { … }
}
```
pascal.taie.language.classes.ClassHierarchy
This class provides class hierarchy information.
- Collection<JClass> getDirectSubclassesOf(JClass): for a given class, returns the classes that directly extend the class.
- Collection<JClass> getDirectSubinterfacesOf(JClass): for a given interface, returns the interfaces that directly extend the interface.
- Collection<JClass> getDirectImplementorsOf(JClass): for a given interface, returns the classes that directly implement the interface.
For example, in this class hierarchy, I, II, and III are interfaces, and the others are classes:
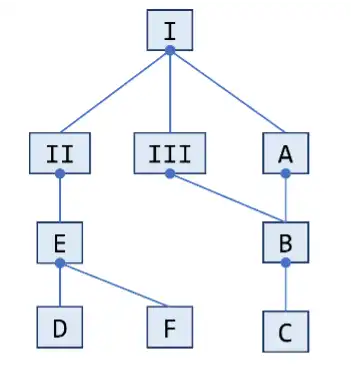
Then we have:
- getDirectSubclassesOf(A) = [B]
- getDirectSubinterfacesOf(I) = [II, III]
- getDirectImplementorsOf(II) = [E]
pascal.taie.analysis.graph.callgraph.CHABuilder
This class builds call graph via class hierarchy analysis. It is incomplete, and you need to finish it as explained in Section 2.2.

2.2 Your Task [Important!]

Your first task is to finish class CHABuilder. Specifically, you will finish three APIs:

JMethod dispatch(JClass,Subsignature)
This method implements the Dispatch function given in page 26 of the slides for Lecture 7. If no satisfying method is found, returns nul
Set<JMethod> resolve(Invoke)
This method implements the Resolve function given in page 33 of the slides for Lecture 7.
Hint:
you could use method CallGraphs.getCallKind(Invoke) to obtain the call kind of a call site.
CallGraph<Invoke, JMethod> buildCallGraph(JMethod)
This method implements the BuildCallGraph algorithm given in page 52 of the slides for Lecture 7.

We have provided code skeletons for the above three APIs, and your task is to fill in the part with comment “TODO – finish me”.

3 Implementing Interprocedural Constant Propagation

3.1 Edge Transfer

Interprocedural constant propagation is very similar to its intraprocedural counterpart. The main difference between them is that interprocedural constant propagation employs edge transfer to handle interprocedural data flows formed by method calls and returns more precisely.

In classic intraprocedural data-flow analysis, take forward analysis as example, the IN fact of a node is computed by directly meeting the OUT facts of all its predecessors:

$IN [B] = ⋃_{P a predecessor of B} OUT [P]$

However, in interprocedural data-flow analysis, for a node, we need to first apply an edge transfer to OUT facts of its predecessors, and then meet the results into its IN fact. For example, in this ICFG fragment discussed in Lecture 7:

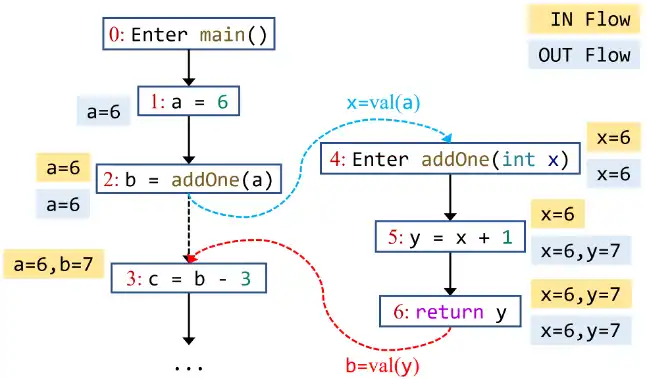
To compute the IN fact of statement 4, i.e., entry node of method addOne(), we need to apply edge transfer for edge 2→4 to convert the OUT fact of statement 2 (a=6) to x=6, and finally meet x=6 into IN fact of statement 4.

To support edge transfer, we define function transferEdge(edge, fact), which takes an edge (edge) on the ICFG and the OUT fact (fact) of source node of the edge as inputs, and outputs the resulting fact. Accordingly, the equation for computing IN facts now changes to

$IN [B] = ⋃_{P a predecessor of B} t r a n s f e r E d g e (P \to B, OUT [P])$

As we have introduced in Lecture 7, in interprocedural constant propagation, you need to define edge transfer functions for four kinds of ICFG edges, as described below:

Normal edge: the edge transfer function is an identity function, i.e. transferEdge(edge, fact) = fact.
Call-to-return edge: for invocation x = m(…), the edge transfer function kills the value of LHS variable, i.e., x, and propagates the values of other variables along the edge. For invocation without LHS variable, e.g., m(…), the edge transfer function is equivalent to an identity function.
Call edge: the edge transfer function passes the values of arguments at a call site to the parameters of its callee(s). Concretely, it obtains the argument values from the OUT fact of the call site, and outputs a fact containing the mapping from parameters of the callee to corresponding values. For example, in Figure 1, transferEdge(2→4, {a=6}) = {x=6}. The result of the transfer function should only contain the values for parameters of the callee (e.g., x of addOne() in Figure 1).
Return edge: the edge transfer function passes the return values of a callee to the LHS variable of the call site. Concretely, it obtains the returned values from the OUT fact of the method exit, and outputs a fact containing the mapping from LHS variable of the call site to corresponding value. For example, in Figure 1, transferEdge(6→3, {x=6,y=7}) = {b=7}. The result of the edge transfer function should only contain the value for LHS variable of the call site (e.g., b at statement 3 in Figure 1). If the call site does not have LHS variable, then the transfer function just returns an empty fact.

We will introduce more information about how to implement these edge transfer functions on Tai-e in the following sections.

3.2 Tai-e Classes You Need to Know

pascal.taie.analysis.graph.icfg.ICFGEdge
This abstract class represents edges in ICFG. It has four subclasses, corresponding to four kinds of ICFG edges:
- pascal.taie.analysis.graph.icfg.NormalEdge
- pascal.taie.analysis.graph.icfg.CallToReturnEdge
- pascal.taie.analysis.graph.icfg.CallEdge
- pascal.taie.analysis.graph.icfg.ReturnEdge
These classes are simple and commented, and you should read the source code to decide how to use them.
pascal.taie.analysis.dataflow.inter.InterDataflowAnalysis
This is the interface of concrete interprocedural data-flow analyses. It has 6 APIs. The first 5 APIs are the same as the ones in DataflowAnalysis, which you have seen in previous assignments, and the last API, transferEdge(), corresponds to the edge transfer function we introduce in Section 3.1. These APIs will be invoked by the interprocedural data-flow analysis solver you will write in this assignment.
pascal.taie.analysis.dataflow.inter.AbstractInterDataflowAnalysis
This abstract class implements InterDataflowAnalysis and provides common functionalities for implementations of InterDataflowAnalysis. Specifically, it dispatches different kinds of ICFG nodes/edges to the specific transfer functions, so that the analysis implementations can directly focus on the specific nodes/edges.
pascal.taie.analysis.dataflow.inter.InterConstantPropagation
This class extends AbstractInterDataflowAnalysis and defines inter-procedural constant propagation. It is incomplete, and you need to finish it as explained in Section 3.3.
pascal.taie.ir.exp.InvokeExp
This class represents invocation expressions in the program. It contains the method reference and arguments of each invocation, and you should read the source code and the comments to decide how to use it.

3.3 Your Task [Important!]

Your second task is to finish the following APIs of InterConstantPropagation:

boolean transferCallNode(Stmt,CPFact,CPFact)
boolean transferNonCallNode(Stmt,CPFact,CPFact)
CPFact transferNormalEdge(NormalEdge,CPFact)
CPFact transferCallToReturnEdge(CallToReturnEdge,CPFact)
CPFact transferCallEdge(LocalEdge,CPFact)
CPFact transferReturnEdge(LocalEdge,CPFact)

This class leverages the logic of intraprocedural constant propagation (it holds an object of ConstantPropagation in its field cp). Thus, to make this class work, you need to finish ConstantPropagation.java. You could copy your implementation from previous assignments. Note that you don’t need to submit ConstantPropagation in this assignment, so that even though your implementation of previous assignments is not entirely correct, it does not affect your score of this assignment.

Hints:

When you implement the transfer*Edge() methods, you should not modify the second parameter, i.e., OUT fact of the source node of the edge.
As introduced in Assignment 2, you could obtain method parameters from class IR. To obtain the IR of a method, you could use API JMethod.getIR().

4 Implementing Interprocedural Worklist Solver

4.1 Algorithm

The algorithm of interprocedural worklist solver is almost the same as intraprocedural worklist solver that you have implemented in Assignment 2. There are only two differences between them:

As explained in Section 3.1, when computing IN fact of a node, interprocedural solver needs to apply edge transfer function (transferEdge) to its incoming edges and the OUT facts of the predecessors.
During initialization, interprocedural solver needs to initialize the IN/OUT facts of all nodes in the program (i.e., all nodes in the ICFG). It should set boundary fact to only the entry nodes of the entry methods of the ICFG (e.g., the main method). The initial facts of entry nodes of other methods are the same as non-entry nodes.

4.2 Tai-e Classes You Need to Know

pascal.taie.analysis.dataflow.fact.DataflowResult
You have seen this class in previous assignments. In this assignment, you will use a DataflowResult object to manages the facts of all nodes in the ICFG. You could get/set IN/OUT facts of nodes in the ICFG through the APIs of this class.
pascal.taie.analysis.graph.icfg.ICFG
This class represents interprocedural control-flow graph of the program. Similar to CFG, it is also iterable, thus you could iterate all nodes of an ICFG via a for loop:
```
ICFG icfg = ...;
for (Node node : icfg) {
    ...
}
```
For more information about ICFG, please read its code and comments.
pascal.taie.analysis.dataflow.inter.InterSolver
This class is the solver for interprocedural data-flow analysis. It is incomplete, and you need to finish it as explained in Section 4.3.

4.3 Your Task [Important!]

Your final task is to finish two APIs of InterSolver:

void initialize()
void doSolve()

Still, you only need to implement a solver for forward analysis as interprocedural constant propagation is forward. You should initialize the IN/OUT facts of ICFG nodes in initialize(), and implement the main part of worklist algorithm in doSolve().

Hint: we have setup the analysis to be solved, the ICFG of the program, and the DataflowResult object for managing the facts, and stored them in fields analysis, icfg, and result of InterSolver, so that you could easily access and manipulate these objects.

5 Run and Test Your Implementation

You can run the analyses as described in Set Up Tai-e Assignments. In this assignment, Tai-e first performs CHA to build a call graph for the program, then constructs ICFG based on the call graph, and finally runs interprocedural constant propagation on the ICFG. To help debugging, it outputs the results of both CHA and interprocedural constant propagation:

#reachable methods: 0

----------Reachable methods:----------

#call graph edges: 0

----------Call graph edges:----------

----------------------------------------

--------------------<Example: void <init>()> (inter-constprop)--------------------

[0@L1] invokespecial %this.<java.lang.Object: void <init>()>(); null

[1@L1] return; null

--------------------<Example: void main(java.lang.String[])> (inter-constprop)--------------------

[0@L5] a = 6; null

[1@L6] temp$1 = invokestatic <Example: int addOne(int)>(a); null

[2@L6] b = temp$1; null

[3@L7] %intconst0 = 3; null

[4@L7] c = b - %intconst0; null

[5@L8] temp$3 = invokestatic <Example: int ten()>(); null

[6@L8] b = temp$3; null

[7@L9] c = a * b; null

[8@L9] return; null

--------------------<Example: int addOne(int)> (inter-constprop)--------------------

[0@L13] %intconst0 = 1; null

[1@L13] y = x + %intconst0; null

[2@L14] return y; null

--------------------<Example: int ten()> (inter-constprop)--------------------

[0@L17] temp$0 = 10; null

[1@L18] return temp$0; null

The above example has been introduced in Lecture 7. The call graph is empty (0 reachable method) and OUT facts are null as you have not finished the analyses yet. After you implement the analyses, the output should be:

#reachable methods: 3

----------Reachable methods:----------

<Example: int addOne(int)>

<Example: int ten()>

<Example: void main(java.lang.String[])>

#call graph edges: 2

----------Call graph edges:----------

<Example: void main(java.lang.String[])>[1@L6] temp$1 = invokestatic <Example: int addOne(int)>(a); -> [<Example: int addOne(int)>]

<Example: void main(java.lang.String[])>[5@L8] temp$3 = invokestatic <Example: int ten()>(); -> [<Example: int ten()>]

----------------------------------------

--------------------<Example: void main(java.lang.String[])> (inter-constprop)--------------------

[0@L5] a = 6; {a=6}

[1@L6] temp$1 = invokestatic <Example: int addOne(int)>(a); {a=6}

[2@L6] b = temp$1; {a=6, b=7, temp$1=7}

[3@L7] %intconst0 = 3; {%intconst0=3, a=6, b=7, temp$1=7}

[4@L7] c = b - %intconst0; {%intconst0=3, a=6, b=7, c=4, temp$1=7}

[5@L8] temp$3 = invokestatic <Example: int ten()>(); {%intconst0=3, a=6, b=7, c=4, temp$1=7}

[6@L8] b = temp$3; {%intconst0=3, a=6, b=10, c=4, temp$1=7, temp$3=10}

[7@L9] c = a * b; {%intconst0=3, a=6, b=10, c=60, temp$1=7, temp$3=10}

[8@L9] return; {%intconst0=3, a=6, b=10, c=60, temp$1=7, temp$3=10}

--------------------<Example: int addOne(int)> (inter-constprop)--------------------

[0@L13] %intconst0 = 1; {%intconst0=1, x=6}

[1@L13] y = x + %intconst0; {%intconst0=1, x=6, y=7}

[2@L14] return y; {%intconst0=1, x=6, y=7}

--------------------<Example: int ten()> (inter-constprop)--------------------

[0@L17] temp$0 = 10; {temp$0=10}

[1@L18] return temp$0; {temp$0=10}

In addition, Tai-e outputs the ICFG of the program it analyzes to folder output/. The ICFGs are stored as .dot files which can be visualized by Graphviz. Note that each ICFG depends on a call graph, thus if you modify CHABuilder, Tai-e may output different ICFGs for the same program.

We provide classes pascal.taie.analysis.graph.callgraph.cha.CHATest and pascal.taie.analysis.dataflow.analysis.constprop.InterCPTest as the test drivers for CHA and interprocedural constant propagation, and you could use them to test your implementation as described in Set Up Tai-e Assignments.

We encourage you to use your implementation of Assignment 2, i.e., intraprocedural constant propagation, to analyze the test cases in this assignment, and observe the precision differences between intra- and inter-procedural analyses.

From this assignment, the analyses you implement are interprocedural analyses, which analyze a program from its entry method, i.e., the main method. Hence, if you want to write a test case for your implementation, please make sure that the input class contains a public static void main(String[]) method.

6 General Requirements

In this assignment, your only goal is correctness. Efficiency is not your concern.
DO NOT distribute the assignment package to any others.
Last but not least, DO NOT plagiarize. The work must be all your own!

7 Submission of Assignment

Your submission should be a zip file, which contains your implementation of

CHABuilder.java
InterConstantPropagation.java
InterSolver.java

8 Grading

You can refer to Grade Your Programming Assignments to use our online judge to grade your completed assignments.

The points will be allocated for correctness. We will use your submission to analyze the given test files from the src/test/resources/ directory, as well as other tests of our own, and compare your output to that of our solution.

Good luck!

# Programming Assignment 4

A4: CHA and Interprocedural Constant Propagation

# 1 Assignment Objectives

# 2 Implementing Class Hierarchy Analysis

# 2.1 Tai-e Classes You Need to Know

# 2.2 Your Task [Important!]

# 3 Implementing Interprocedural Constant Propagation

# 3.1 Edge Transfer

# 3.2 Tai-e Classes You Need to Know

# 3.3 Your Task [Important!]

# 4 Implementing Interprocedural Worklist Solver

# 4.1 Algorithm

# 4.2 Tai-e Classes You Need to Know

# 4.3 Your Task [Important!]

# 5 Run and Test Your Implementation

# 6 General Requirements

# 7 Submission of Assignment

# 8 Grading

Programming Assignment 4

1 Assignment Objectives

2 Implementing Class Hierarchy Analysis

2.1 Tai-e Classes You Need to Know

2.2 Your Task [Important!]

3 Implementing Interprocedural Constant Propagation

3.1 Edge Transfer

3.2 Tai-e Classes You Need to Know

3.3 Your Task [Important!]

4 Implementing Interprocedural Worklist Solver

4.1 Algorithm

4.2 Tai-e Classes You Need to Know

4.3 Your Task [Important!]

5 Run and Test Your Implementation

6 General Requirements

7 Submission of Assignment

8 Grading